rueki
Eigen Values, Eigen Vectors 본문
1. 정의
Ax = λx
대부분의 Vector들은 Ax에 의해서 다른 방향을 가지게 된다.
즉, Ax는 원래 x와는 다른 방향으로 변환이 된다.
여기서 Ax는 Square Matrix A에 의해 변환되는 Vector x라고 이해하면 될 것이다.
일반적으로는 Ax는 입력 벡터 x와는 다른 방향으로 변환이 된다.
But, 변환된 Vector 중, 변환되기 전 벡터 x와 평행한 vector가 존재하는데,
여기서 A애 의해 변환 전, 변환후가 평행한 Vector를 Eigen Vector라고 한다.
-
Eigen Vector 정리
: Linear System A에 의해 변환되는 수 많은 벡터들 중에,
곱하기 전과 후의 벡터 방향이똑같은 벡터이다.
크기는 스칼라 및 상수 배만큼 다를 수가 있다.
상수는 λ(lambda)로 표현할 수가 있다.
위의 식에서 미지수는 x와 λ 이며, Eigen Vector는 Vector x이다.
2. Eigen Value와 Vector를 어떻게 구할 것인가?
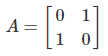

위와 같이 A와 x값이 주어졌을 때 λ값은 무엇일까?
Ax = λx 를 이용해서 풀어보자.

Eigen value는 1인 것을 알 수가 있다.
그럼 만약 λ값이 -1일 때, x값은 무엇일까?


Eigen Value의 합은 Diagonal matrix(대각 행렬) 성분의 합과 같다.
-> sum of λ = sum diagonal of Matrix A
3. Eigen Value와 Eigen Vector를 찾는 방법
Ax = λx -> Ax - λx = 0

행렬 A가 위의 조건을 만족할 때, λ는 A의 Eigen Value임을 나타내기 위해서는
det(A-λI)=0 이어야한다.
참고 - 2차원 행렬 A에서의 행렬식 det(A)를 구하는 방법

det (A) = ad-bc
Ax = λx를 만족하는 0이 아닌 Vector v가 존재하고 v ∈ R이라고 할때,
(A - λI)(v) =0 이 성립된다.
1) characteristic polynomial (특성 다항식)을 이용해서 Eigen value 계산
특성다항식은 아래와 같다.


이를 계산하면 Eigen Value는 3과 -1이 나오는데 자세한 과정은 새로운 예제로 설명을 이어가겠다.
2) Eigen value를 이용해서 Eigen Vector 구하기


행렬 A의 대각성분의 합과 Eigen value의 합이 동일함을 알 수가 있다.
이제 A-λI 에 Eigen value를 대입해서 계산해보자.
- Eigen Value가 4인것에 대한 Eigen vector

lambda 값에 4를 넣고 연산한 행렬이며 특성다항식을 만족해야한다.

결과가 0이 나오는 벡터 x의 값이 즉 Eigen Vector이며 결과 값은 아래와 같다.

- Eigen Value가 2인것에 대한 Eigen vector


2번에서의 예제에서 구한 Eigen value,vector와 방금 전의 예제에서
구한 것을 비교해보자.

3번의 행렬은 1번의 행렬에서 3I를 더한 것과 같다.
그러면 두 행렬의 각각의 Eigen value와 Eigen vector 간의 관계는
어떻게 되는지 살펴보자.
각 고유값 간의 차는 3이고 Eigen vector는 동일한 것을 확인할 수가 있다.
이를 통해 아래와 같이 정리할 수가 있다.
※ 정리

'선형대수' 카테고리의 다른 글
| Matrix 기본 연산 (0) | 2021.10.13 |
|---|---|
| Linear equation, System (0) | 2021.10.01 |
| 벡터의 정의 및 성질 (0) | 2020.05.19 |
| 9. 선형변환과 행렬 (0) | 2020.05.01 |
| 벡터공간의 차원과 4가지 Sub Vector space (0) | 2020.04.19 |


