rueki
문서 유사도 - 그 외의 유사도 기법들 본문
728x90
반응형
1. 유클리드 거리

두 개의 점 P, q가 각각의 좌표를 가질 때, 두 점 사이의 거리를 계산하는 유클리드 공식이다.

2차원에서 두 점 p와 q사이의 거리를 구하는 것을 나타내었다.
두 점 사이의 유클리드 거리 공식은 피타고라스를 통해 구할 수 있다.
넘파이를 이용해서 구현해보자
import numpy as np
def dist(x,y):
return np.sqrt(np.sum((x-y)**2))
doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))
print(dist(doc1,docQ))
print(dist(doc2,docQ))
print(dist(doc3,docQ))
2.23606797749979
3.1622776601683795
2.449489742783178값이 제일 작게나온 것이 문서간의 거리가 가장 가깝다는 것이다.
즉 1번 문서와 문서Q가 가장 유사하다.
2. 자카드 유사도(Jaccard similarity)
합집합에서 교집합의 비율을 구하면 두 집합간의 유사도를 구할 수 있다는 것이 자카드 유사도의 정의이다.
0과 1사이의 값을 가지며, 두 집합이 동일하다면 1, 공통 원소가 없다면 0의 값을 갖는다.
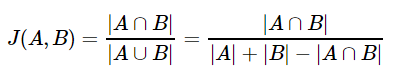
간단한 예로 진행을 해보자
doc1 = "apple banana everyone like likey watch card holder"
doc2 = "apple banana coupon passport love you"
tokenzied_doc1 = doc1.split()
tokenzied_doc2 = doc2.split()
print(tokenzied_doc1)
print(tokenzied_doc2)['apple', 'banana', 'everyone', 'like', 'likey', 'watch', 'card', 'holder']
['apple', 'banana', 'coupon', 'passport', 'love', 'you']임의로 split을 통해 토큰화를 진행해보았고 두 집합 간의 합집합을 구해보자
union = set(tokenzied_doc1).union(set(tokenzied_doc2))
print(union){'everyone', 'coupon', 'banana', 'watch', 'apple', 'likey', 'like', 'love', 'you', 'card', 'passport', 'holder'}개수는 총 12개이다. 이제 교집합을 구해보자
intersection = set(tokenzied_doc1).intersection(set(tokenzied_doc2))
print(intersection){'banana', 'apple'}이제 교집합을 합집합으로 나누면, 자카드 유사도가 나오게 된다.
print(len(intersection)/len(union))
0.16666666666666666이로써 자카드 유사도까지 구해보았다.
728x90
반응형
'DL > NLP' 카테고리의 다른 글
| 토픽 모델링 - 잠재 디리클레 할당(Latent Dirichlet Allocation) (0) | 2019.07.03 |
|---|---|
| 토픽 모델링 - 잠재 의미 분석(Latent Semantic Analysis, LSA) (0) | 2019.07.03 |
| 문서 유사도 - 코사인 유사도(Cosine Similarity) (0) | 2019.07.03 |
| 카운트 기반 단어 표현 - TF-IDF (0) | 2019.07.02 |
| 카운트 기반 단어 표현 - 문서 단어 행렬(Document-Term Matrix, DTM) (0) | 2019.07.02 |
Comments




