rueki
토픽 모델링 - 잠재 의미 분석(Latent Semantic Analysis, LSA) 본문
자연어 처리에서 토픽은 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나이며,
텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법이다.
Bow에 기반한 DTM이나 TF-IDF는 기본적으로 단어의 빈도 수를 이용한 수치화 방법으로
단어의 의미는 고려하지 않았다. 이에 대한 대안으로 나온 것이 잠재 의미 분석(LSA)이다.
LSA를 이해하기 위해서는 선형대수의 특이값 분해(SVD)를 이해해야한다.
특이값 분해(SVD)는 실수 벡터 공간에 한정하여 내용을 설명한다.
A가 m × n 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해(decomposition)하는 것을 말한다.

직교행렬 : 자신과 자신의 전치 행렬의 곱 또는 이를 반대로 곱한 결과가 단위행렬이 되는 행렬
대각행렬 : 주 대각선을 제외한 곳의 원소가 모두 0인 행렬
대각행렬에서는 대각원소 값을 특이값(singular value)라고 한다.
1 )전치행렬(Transposed Matrix)
원래의 행렬에서 행과 열을 바꾼 행렬이다.

2) 단위행렬(Identity Matrix)
주 대각원소의 원소가 모두 1이며 나머지 원소는 0인 정사각 행렬

3) 역행렬(Inverse Matrix)
자신과 어떠한 행렬을 곱했을 때 결과가 단위행렬이 나온다면 그 행렬을 역행렬이라 한다.

4) 직교 행렬(Orthogonal martix)
n x n 행렬 A에 대해 A × A^T= I 를 만족하면서, A^T x A = I 를 만족하는 행렬 A를 직교행렬이라고 한다.
5) 대각 행렬(Diagonal matrix)
주 대각선을 제외한 곳의 원소가 모두 0인 행렬을 말한다.
주대각원소를 행렬 A의 특이값으로 정의한다.

LSA에서는 풀 SVD에서 나온 3개의 행렬에서 일부 벡터를 삭제시킨 절단된 SVD(truncaated SVD)를 사용하게 된다.

절단된 SVD는 대각행렬Σ의 대각원소 값 중에서 상위값 t개만 남게 된다.
U와 V행렬은 t열까지만 남긴다. 즉 t값은 찾고자하는 토픽의 수를 반영한 하이퍼 파라미터값이 된다.
*하이퍼 파라미터 : 사용자가 직접 값을 선택하며 성능에 영향을 주는 매개변수
t값을 작게 잡아야 노이즈를 제거할 수 있고, 크게 잡으면 기존 행렬로 부터 다양한 의미를 가져갈 수 있다.
절단된 SVD는 데이터의 차원을 줄이게 되면서, 계산 비용이 낮아지는 효과를 얻을 수 있다.
이는 자연어 처리에서, 설명력이 낮은 정보는 삭제하고, 설명력이 높은 정보를 남긴다라는 의미가 있으며,
즉, 기존 행렬에서는 드러나지 않은 심층적인 의미를 확인할 수가 있다.
LSA(Latent Semantic Analysis) 잠재 의미 분석은 TF-IDF 행렬 및 DTM에서 절단된 SVD를 사용해서
차원을 축소시키고, 단어들의 잠재적 의미를 끌어낸다.
예제를 통해 알아보자
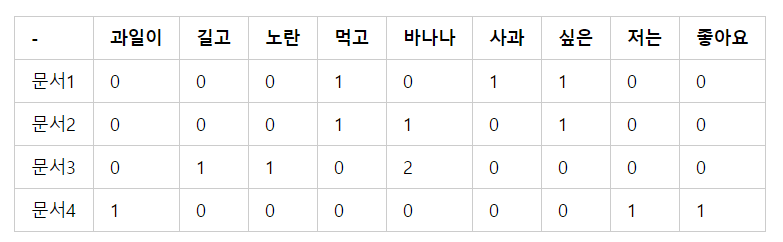
U, s, VT = np.linalg.svd(A, full_matrices=True)
print(U.round(2))
np.shape(U)U - 직교행렬 s - 대각행렬 VT - 전치행렬
[[-0.24 0.75 0. -0.62]
[-0.51 0.44 -0. 0.74]
[-0.83 -0.49 -0. -0.27]
[-0. -0. 1. 0. ]]
(4, 4)4x4 의 직교행렬 U를 생성했다.
print(s.round(2))
np.shape(s)
[2.69 2.05 1.73 0.77]
(4,)linalg.svd()는 특이값 분해의 결과로 특이값 리스트를 반환한다. 그래서 수식의 형식을 바꿔주어야 한다.
S = np.zeros((4,9))
S[:4, :4] = np.diag(s)
print(S.round(2))
np.shape(S)
[[2.69 0. 0. 0. 0. 0. 0. 0. 0. ]
[0. 2.05 0. 0. 0. 0. 0. 0. 0. ]
[0. 0. 1.73 0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0.77 0. 0. 0. 0. 0. ]]
(4, 9)S 행렬을 초기의 형태 4x9 형태로 하고 앞서 뽑아낸 특이값을 대각으로 삽입하였다.
print(VT.round(2))
np.shape(VT)[[-0. -0.31 -0.31 -0.28 -0.8 -0.09 -0.28 -0. -0. ]
[ 0. -0.24 -0.24 0.58 -0.26 0.37 0.58 -0. -0. ]
[ 0.58 -0. 0. 0. -0. 0. -0. 0.58 0.58]
[ 0. -0.35 -0.35 0.16 0.25 -0.8 0.16 -0. -0. ]
[-0. -0.78 -0.01 -0.2 0.4 0.4 -0.2 0. 0. ]
[-0.29 0.31 -0.78 -0.24 0.23 0.23 0.01 0.14 0.14]
[-0.29 -0.1 0.26 -0.59 -0.08 -0.08 0.66 0.14 0.14]
[-0.5 -0.06 0.15 0.24 -0.05 -0.05 -0.19 0.75 -0.25]
[-0.5 -0.06 0.15 0.24 -0.05 -0.05 -0.19 -0.25 0.75]]
(9, 9)이로써 U, S, VT를 생성했다. 전부 곱하면 기존의 A가 나와야한다.
Numpy의 allclose()는 2개의 행렬이 동일하면 True를 리턴한다.
np.allclose(A, np.dot(np.dot(U,S),VT).round(2))True이제 t값을 정해서 절단된 SVD를 수행해보자
t를 2로 설정하고 특이값 중 2개만 남기고 제거해보자
S = S[:2,:2]
print(S.round(2))
U=U[:,:2]
print(U.round(2))
VT = VT[:2,:]
print(VT.round(2))[[2.69 0. ]
[0. 2.05]]
[[-0.24 0.75]
[-0.51 0.44]
[-0.83 -0.49]
[-0. -0. ]]
[[-0. -0.31 -0.31 -0.28 -0.8 -0.09 -0.28 -0. -0. ]
[ 0. -0.24 -0.24 0.58 -0.26 0.37 0.58 -0. -0. ]]U, S, VT의 절단된 SVD를 구해보았다. 이제 세 행렬을 곱하면 기존의 A와는 다른 결과가 나올 것이다.
A_prime = np.dot(np.dot(U,S),VT)
print(A)
print(A_prime.round(2))[[0 0 0 1 0 1 1 0 0]
[0 0 0 1 1 0 1 0 0]
[0 1 1 0 2 0 0 0 0]
[1 0 0 0 0 0 0 1 1]]
[[ 0. -0.17 -0.17 1.08 0.12 0.62 1.08 -0. -0. ]
[ 0. 0.2 0.2 0.91 0.86 0.45 0.91 0. 0. ]
[ 0. 0.93 0.93 0.03 2.05 -0.17 0.03 0. 0. ]
[ 0. 0. 0. 0. 0. -0. 0. 0. 0. ]]축소된 U는 4x2 의 크기를 가지는데, 문서의 개수 x 토픽의 수 t의 크기이다.
4개의 문서 각각을 2개의 값으로 표현하고 있다.
즉, U의 각 행은 잠재의미를 표현하기 위한 수치화 된 각각의 문서 벡터라고 볼 수 있다.
축소된 VT는 2x9의 크기를 가지는데 토픽의 수 t x 단어의 개수 크기이다.
VT의 각 열은 잠재 의미를 표현하기 위해 수치화 된 각각의 단어 벡터라고 볼 수 있다.
'DL > NLP' 카테고리의 다른 글
| 워드 임베딩 (0) | 2019.07.04 |
|---|---|
| 토픽 모델링 - 잠재 디리클레 할당(Latent Dirichlet Allocation) (0) | 2019.07.03 |
| 문서 유사도 - 그 외의 유사도 기법들 (0) | 2019.07.03 |
| 문서 유사도 - 코사인 유사도(Cosine Similarity) (0) | 2019.07.03 |
| 카운트 기반 단어 표현 - TF-IDF (0) | 2019.07.02 |




