rueki
벡터공간의 차원과 4가지 Sub Vector space 본문
본 게시글은 한양대학교 이상화 교수님의 kocw 선형대수학 강의를 정리한 게시글입니다.
선형독립(Linear Independence)
$c_{1}v_{1} + c_{2}v_{2} + ... + c_{n}v_{n} = 0$ 의 식을 가지는데, 결과적으로는 $Ax = b$ 의 선형결합 구조를 띈다.
즉, Linear Combination을 했을 때, 결과가 Zero Vector가 나올 경우를 선형독립이라고 한다.
이러한 결과가 나오기 위해서는 Scalar C가 0의 값을 가지면 된다.
나머지 Vector로 임의 vector를 선형 결합으로 정의할 수 없게 된다.
예를 들어서 살펴보자.
$V_{1}=\begin{bmatrix}1\\0\\0\end{bmatrix}, V_{2}=\begin{bmatrix}0\\1\\0\end{bmatrix}, V_{3}=\begin{bmatrix}0\\0\\1\end{bmatrix} \in R^{3}$
위와 같이 세가지 벡터가 존재하고 3차원의 실수 벡터에 포함될 때, 선형독립임을 나타내고자 할 때,
아래의 수식으로 표현할 수가 있다.

이제 여기서 Span이라는 개념이 등장하게 된다.
Span : Vector들의 집합이 선형 결합으로 Vector Space를 생성하는데,
이는 모든 선형 결합 과정을 거치게 된다.
벡터들의 집합이 Vector Space를 Span한다라고 설명할 수 있다.
$$V_{1} , V_{2}, V_{3} span R^{3}$$
$V_{1}=\begin{bmatrix}1\\0\\0\end{bmatrix}, V_{2}=\begin{bmatrix}0\\1\\0\end{bmatrix}, V_{3}=\begin{bmatrix}1\\1\\1\end{bmatrix}$ span $R^{3}$
: span 할 수 있는 linear Independent Vector 집합이며, Unique 한 Solution은 아니다.

위와 같은 벡터가 추가로 존재할 경우, 이 역시 $R^{3}$ 공간을 span 할 수 있다.
여기까지 선형 독립의 정의와 span에 대해 간략하게 알아보았고,
이제 선형 독립에 중점을 두고 더 알아보자.
선형 독립 Vector가 주어졌을 때, linear Combination 조합은 Unique하게 존재하며,
이는 하나의 조합으로만 표현이 가능하다.
연장되는 개념으로 이제 Basis가 등장한다.
Basis (기저) => Vector들의 집합
: Vector space를 span할 수 있는 최소한의 Vector의 수이며,
최대한 많은 선형 독립 Vector들의 집합이다.
$V_{1}=\begin{bmatrix}1\\0\\0\end{bmatrix}, V_{2}=\begin{bmatrix}0\\1\\0\end{bmatrix}, V_{3}=\begin{bmatrix}0\\0\\1\end{bmatrix}$ span $R^{3}$ 라고 할 때,
$V_{1}=\begin{bmatrix}1\\0\\0\end{bmatrix}, V_{2}=\begin{bmatrix}1\\1\\0\end{bmatrix}, V_{3}=\begin{bmatrix}1\\1\\1\end{bmatrix}$ 가 주어졌다.
위의 벡터들 즉, Basis는 Unique하지 않다. 선형 결합으로 unique한 solution이 존재할 수는 있으나,
Vector space에 있어 unique하지는 않다.
Basis vector를 Linear independence하게 고른다고 할 때 어떠한 Vector를 구하면 될까?
정답은 두 벡터를 내적했을 때 수직이 되는 벡터를 고르면 된다.
$V_{i} \cdot V_{j} = 0$ , $i \neq j$
$v_{1}, v_{2}, ... ,v_{n}$ 이 있을 때, $b = c_{1}v_{1} + c_{2}v_{2} + ... + c_{n}v_{n}$ 라고하자.
이럴 때 $v_{k} \cdot b = c_{k}b_{k}$ 여야 한다. 구조는 역시 Ax=b의 구조를 가진다.
$\begin{bmatrix}\\\\v_{1}, ..., v_{n}\\\\\\ \end{bmatrix}\begin{bmatrix}c_{1}\\.\\.\\.\\c_{n}\\ \end{bmatrix} = b$
Vector space의 차원은 선형 독립 Vector의 수라고 할 수가 있다.
행렬 A의 Rank의 정의는 아래와 같다
-> Linear independent한 Column Vector의 수
-> Linear independent한 Row Vector 수
-> Pivot의 수
위의 정의에서 연결되서 행렬 A (m by n)에 대한 4가지 Subspace를 설명하고자 한다.
1) Column Space
$C(A)$ : Column Vector의 Linear Combination
2) Null Space
$N(A)$ : ${x | Ax = 0} \subset R^{n}$
3) Row Space
$C(A^{T})$ : Linear Combination of Row vectors, $\subset R^{n}$
4) Left Null space
$N(A^{T})$ : ${y | A^{T}y = 0} \subset R^{m}$
Ex)
$A=\begin{bmatrix}1 & 0 &0 \\0 & 0 & 0 \end{bmatrix}$
Column Space $C(A)$
$c\begin{bmatrix}1 \\0 \end{bmatrix} \subset R^{2}$
Null Space $N(A)$
$x_{2}\begin{bmatrix}0\\1 \\0 \end{bmatrix} + x_{3}\begin{bmatrix}0\\0\\1 \end{bmatrix} \subset R^{3}$
Row Space $C(A^{T})$

Left Null Space $N(A^{T})$
$\begin{bmatrix}1 & 0 \\0 & 0\\0 & 0 \end{bmatrix}
\begin{bmatrix}x_{1} \\y_{2} \end{bmatrix}$
$N(A^{T}) = y_{2}\begin{bmatrix}0 \\1 \end{bmatrix}$
m by n인 행렬 A가 존재할 때 아래의 식이 성립된다.
$Dim(C(A)) + Dim(N(A^{T})) = m$
=> r + m - r = m (r : rank)
$Dim(C(A^{T})) + Dim(N(A)) = n$
Ex)
$A = \begin{bmatrix}1 & 2 \\3 & 6 \end{bmatrix}, A^{T} = \begin{bmatrix}1 & 3 \\2 & 6 \end{bmatrix}$
Column Space $C(A)$
$c\begin{bmatrix}1\\3\end{bmatrix}$
Null Space $N(A)$
$x_{2}\begin{bmatrix}-2\\1\end{bmatrix}$
Row Space $C(A^{T})$
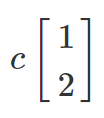
Left Null space $N(A^{T})$
$N(A^{T}) = y_{2}\begin{bmatrix}-3 \\1 \end{bmatrix}$
추가적으로 m<n 인 경우와 m>n 인 경우를 나누어서 볼 건데, 순서대로 Rigth inverse, Left Inverse라고 한다.
1) Right Inverse (m<n)
$AA^{-1} = I_{m,m}$
$A^{-1}A$ 인 경우에는 아래와 같은 행렬 결과를 받게 된다.
| I | 0 | |
| 0 | ||
| 0 | 0 | 0 |
2) Left Inverse (m>n)
$AA^{-1} = I_{n,n}$
$A^{-1}Ax = A^{-1}b$
=> $X = A^{-1}b$
'선형대수' 카테고리의 다른 글
| Linear equation, System (0) | 2021.10.01 |
|---|---|
| Eigen Values, Eigen Vectors (0) | 2020.06.19 |
| 벡터의 정의 및 성질 (0) | 2020.05.19 |
| 9. 선형변환과 행렬 (0) | 2020.05.01 |
| 7. 벡터의 선형독립, 기저 Vector (0) | 2020.04.12 |




